所有内容来自 http://ml-class.org 。最后一部分尚未完成。

线性回归

元线性回归中的多个输入变量 \(x_i\) 的取值域可能差异较大，比如一个是 \(\begin{bmatrix} 0.01 & 0.1 \end{bmatrix}\)，而另一个是 \(\begin{bmatrix} 100 & 10000 \end{bmatrix}\) 。这带来的问题是，多维空间中的损耗函数在各个方向上的梯度分布不均匀，甚至差异极大。那么，当采用梯度下降来优化参数时，可能会在某个方向上浪费过多的资源，导致收敛速度较慢。

该问题一般使用特征缩放（Feature Scaling）和均值归一（Mean Normalization）解决。特征缩放将各个输入处于这些输入的阈值，均值归一将各个输入减去所有输入的均值。结合起来得到

\[x_i' = \frac{x_i - u_i}{x_{\mathrm{max}} - x_{\mathrm{min}}}.\]

不当的学习速率可能会影响模型的收敛。当学习速率过大时，训练的准确性可能会一直增长，或是持续地抖动。这是因为，在采用梯度下降优化时，过大的学习速率使得我们「不断」地跨过了「山谷」。由于在「山坡」上的梯度更高，使得下次迈向更高的「山坡」，如下图。学习速率过低会导致收敛太慢。经验性的学习速率为 0.01 或更低，调整的幅度为 3X。

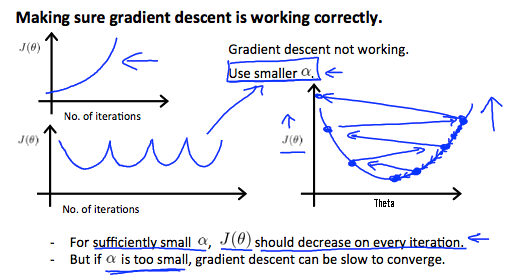
Learning Rate

梯度下降优化方法需要缓慢地逼近局部最小值，而正规方程可以直接找到极小值，省去大量的迭代计算。对于线性回归问题 \(\textbf{Xθ} = \textbf{y}\) ，有正规方程（Normal Equation）\(\textbf{θ}=(\textbf{X}^\mathrm{T}\textbf{X})^{−1}\textbf{X}^\mathrm{T}\textbf{y}\) 。然而，当参数数量比较大时（比如有 10000 个），正规方程的求解复杂度 \(O(n^3)\) 是不可接受的（主要是求矩阵逆开销太大），这时要用梯度下降。

逻辑回归

对于分类（classification）问题而言，应用线性回归是有问题的。分类问题可以抽象成输出为 0 和 1 ，而线性回归的预测结果一般会有 >1 或 <0 ；并且，线性回归对额外数据敏感，不能很好地拟合分类问题（如下图）。此时，我们需要用 sigmod/logistic 函数来拟合。

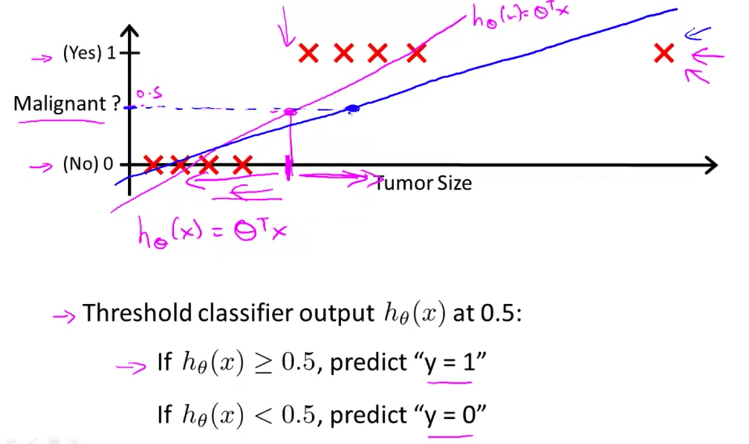
defect-of-linear-regression-in-classification

逻辑回归描述的是对于给定的 \(\bf{x}\) ，\(\bf{\theta}\) 将输出 \(y\) 参数化为 1 的概率—— \(P(y=1 \vert \textbf{x};\bf{\theta})\) 。

\[h_\theta(\textbf{x})=g(\theta^\mathrm{T}\textbf{x})\] \[g(z)=\frac{1}{1+e^{-z}}\]

决策边界（decision boundary）是二分类的「分界线」。它并不总是线性的，如下图。

decision-boundary

如果我们将上文中应用于线性回归的 \(L^2\) 误差函数，应用于逻辑回归这样的分类问题，那么我们的误差函数可能是无法收敛的（因为有太多的局部最小值）。

适合于逻辑回归的损耗函数定义为：

\[J(\theta) = \dfrac{1}{m} \sum_{i=1}^m \mathrm{Cost}(h_\theta(x^{(i)}),y^{(i)})\] \[\begin{align} \mathrm{Cost}(h_\theta(x),y) &= \left\{\begin{array} -\log(h_\theta(x)); & \text{if y = 1} \\\\ -\log(1-h_\theta(x)); & \text{if y = 0} \end{array}\right. \\\\ &= y^{(i)}\log (h_\theta (x^{(i)})) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)})) \end{align}\]

在通过最小化 \(J(\theta)\) 求解 \(\theta\) 时，除了梯度下降外还有很多更加高效的算法：Conjugate dradient, BFGS, L-BFGS。但它们过于复杂，我们一般直接使用相关的库函数，如 Octave 中的 fminunc 。

对于多元分类问题，我们可以将其转化为若干个二分类问题，并分别训练。在推理时，选择「信心」最足的那个二分类作为结果。

神经网络

当将线性回归或逻辑回归应用于复杂问题时，我们需要的参数数量几乎相对于特征数量成 \(O(n^2)\) 增长。另一方面，人们发现大脑具有极高的灵活性（原本处理听觉的区域在连接视觉神经后可以处理视觉），乃至出现下图中的一些实验性应用。

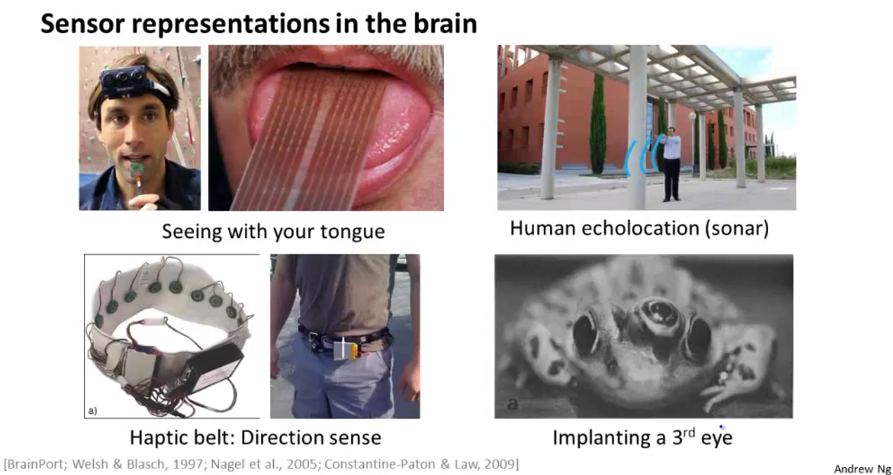
brain-expr

神经网络的一个示例如下图，其中的激活函数为 logistic/sigmod 函数。可以看到，每个神经元和它的前驱节点之间的关系是非常结构化的，数学描述也非常一致。类似于线性回归，我们通常会增加一个输入 \(x_0\)（在第 \(i\) 层中是 \(a_0^{(i)}\)）作为偏置（bias）。其中的 \(\Theta_{ij}^k\) 是从 k-1 层中第 j 个神经元到第 k 层中第 i 个神经元的链接的权重/参数。

neural-network

对于上图中的网络，我们可以引入 \(\textbf{z}^{(j)} = \Theta^{(j-1)}\textbf{a}^{(j-1)}\)，其中 \(j\) 表示网络中的层数。那么有 \(\textbf{a}^{(j)} = g(\textbf{z}^{(j)})\)，和最终的输出 \(\textbf{h}_\Theta(\textbf{x}) = \textbf{a}^{(j+1)} = g(\textbf{z}^{(j+1)})\) 。针对网络中的每个神经元，我们都可以将其看做是一个简单的逻辑回归问题；那么神经网络本身就是由若干个逻辑回归分类器链接而成。

神经网络最初的特别之处在于它能学习 XOR ，一个这样的网络而具体实现如下图。可以看到，神经网络可以将一些相对较为简单的函数组合起来，形成强大的表达能力。

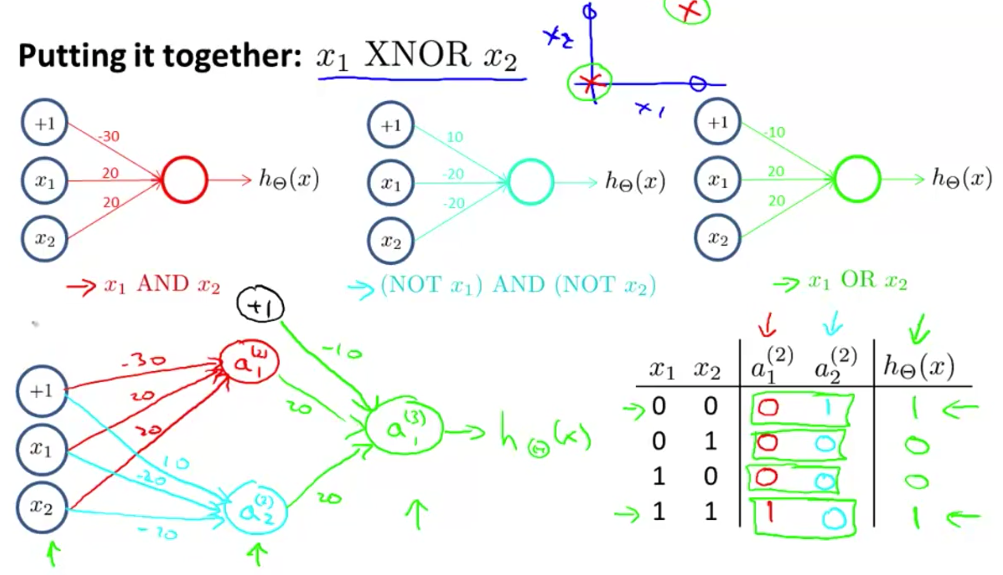
nn-xnor

神经网络的误差函数为：

\[\begin{gather*} J(\Theta) = - \frac{1}{m} \sum_{i=1}^m \sum_{k=1}^K \left[y^{(i)}_k \log ((h_\Theta (x^{(i)}))_k) + (1 - y^{(i)}_k)\log (1 - (h_\Theta(x^{(i)}))_k)\right] + \frac{\lambda}{2m}\sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}} ( \Theta_{j,i}^{(l)})^2\end{gather*}\]

反向传播是神经网络中比较流行的计算误差梯度的方法，其具体（一种易于计算的方法）计算步骤如下图。

backpropagation

在反向传播的计算实践中，我们可能会将参数矩阵 \(\Theta\) 展开成向量（因为 fminunc 这样的函数要求参数为向量？）。具体的方法如下。

impl-of-backpropagation

可以看到，反向传播算法的计算还是比较复杂的，那么我们在实践中就很容易出错。通常我们可以「手动」计算梯度（计算方式如下）来检查通过误差函数得到的梯度是否正确（两者接近或相等）。不过，这种计算比较费时，在正式训练时要记得关掉。

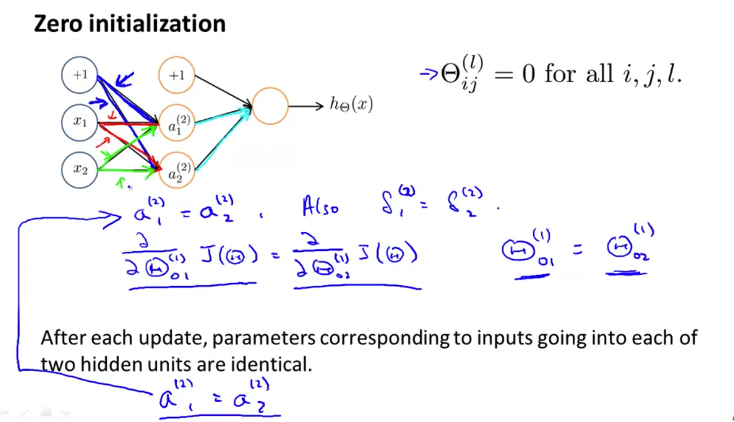
\[\dfrac{\partial}{\partial\Theta_j}J(\Theta) \approx \dfrac{J(\Theta_1, \dots, \Theta_j + \epsilon, \dots, \Theta_n) - J(\Theta_1, \dots, \Theta_j - \epsilon, \dots, \Theta_n)}{2\epsilon}\]

训练中的另一个需要注意的问题是要随机地初始化参数。考虑所有节点（也可以是部分）的参数都是一样的，如下图中相同颜色的链接。那么学习时，他们得到的更新也是一样的。这样的情况称作「对称性」，它使得网络中实际起作用的节点数变少了。随机地初始化参数可以解决这一问题。

rand-param-init

关于机器学习应用的建议

当我们在预测中发现错误率过高时，应当考虑改进我们的算法。改进的几种基本方法包括：获取更多的训练数据、减少/增加特征、增加多项式特征（即 \(x_1^2, x_2^2, x_1x_2, ...\)）、调整正则化参数 \(\lambda\) 等。具体选择哪一种要结合实际情况。

正规化

当过拟合发生时，我们一般裁剪特征数量（手动或自动），或是采用正规化（Regularization）。正规化「压缩」特征，使得拟合不会被个别特征过度影响，如下图。

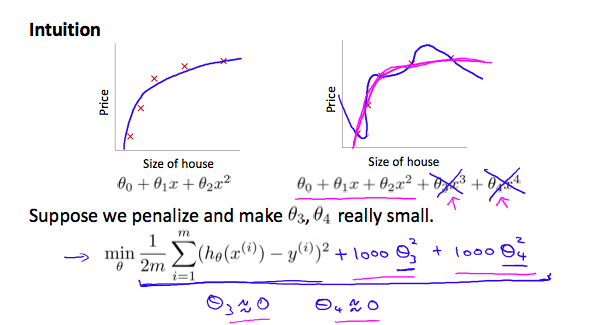
intuition-of-why-regularization

\[J(\theta) = \frac{1}{2m}\left[\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2 + \lambda\sum_{j=1}^n\theta_j^2\right]\]

上面的公式是正规化的数学表示，其中 \(\lambda\) 是用于调整正规化程度「正规化参数」（regularization parameter）。该参数不能过大，否则 \(\theta\) 会趋近于 0 （假说失去表达能力），从而发生欠拟合。一般以「两倍」的速度来调整 \(\lambda\) 。当 \(\lambda\) 变换时，训练集和验证集的损失函数变换如下图。

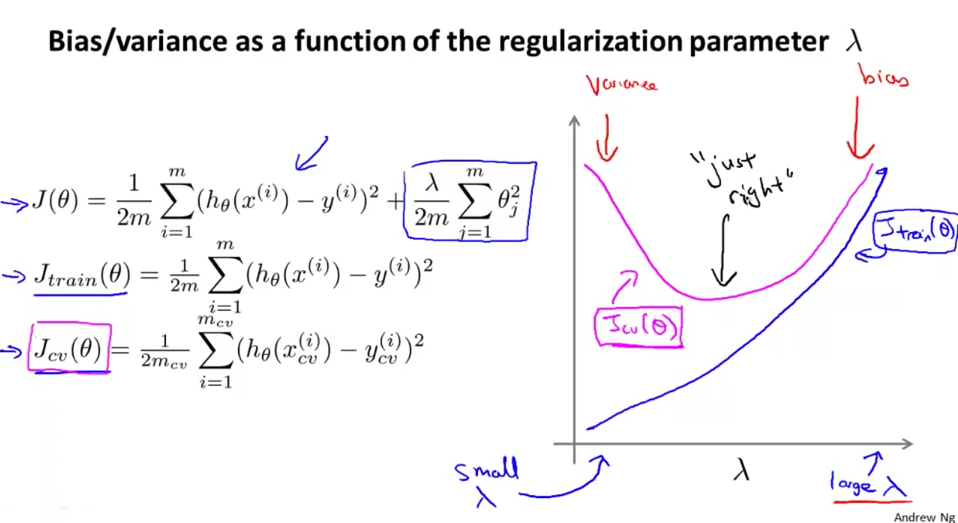
lambda-and-cost

对于线性回归，用梯度下降求解 \(\theta\) 时，在每次迭代中， \(\theta\) 的「原始值」都比没有正规化要保留得少，那么直觉上最终的 \(\theta\) 也会比较小。当用正规方程求解时（\(\theta = \left( X^TX + \lambda \cdot L \right)^{-1} X^Ty\)，其中 \(L = \begin{bmatrix} 0 & & & & \newline & 1 & & & \newline & & & \ddots & \newline & & & & 1 \newline\end{bmatrix}\)），其中的逆矩阵部分会必然可逆，这是正规化的另一个好处。逻辑回归中的梯度下降具有类似性质。注意，我们不对 \(\theta_0\) 使用正规化（尽管这对最后的拟合影响不大）。

模型容量与错误率

下面继续看模型容量和训练样本以及误差率的关系。当模型容量较低（即欠拟合）时，训练集和验证集上的错误率都比较高。而且，由于模型容量低，少量的数据便使得模型达到拟合极限，错误率几乎不再变化。这时收集更多的样本意义不大。

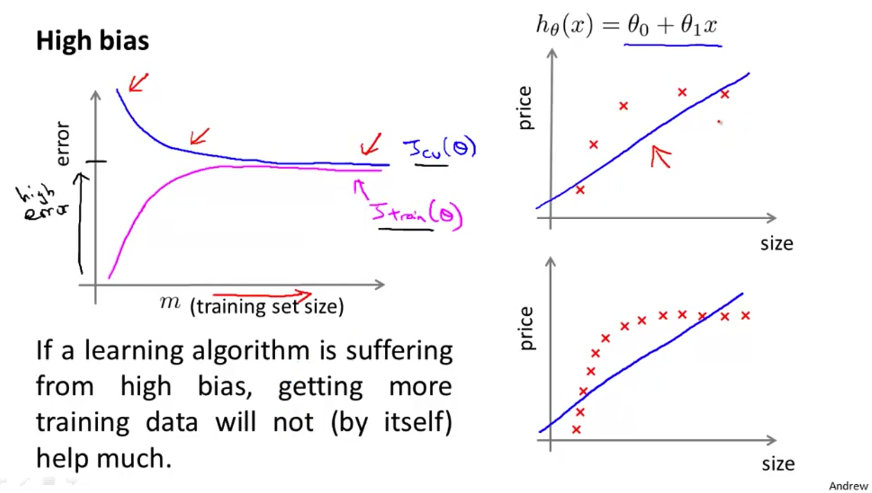
learning-curve-bias

当模型容量过高时容易发生过拟合，此时训练集误差和测试集差距较大。随着数据量的不断增长，模型的预测会逐步改进，以至于最后可能得到很好的结果。不过这付出的代价可能不太值得。

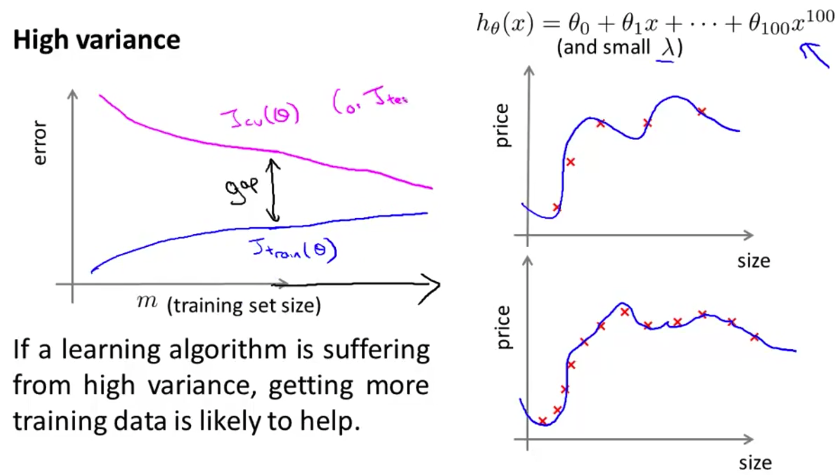
learning-curve-variance

机器学习系统的设计

当面对一个新的机器学习问题时，往往可以「三步走」：

  • 用最熟悉和最简单的算法做一个快速实现，并做交叉验证。
  • 画出学习曲线，看看增加特征或样本等是否有帮助。
  • 分析验证集中被错误分类的样本，确定下一步优化的方向。

结合上一小节的分析，我们可以有如下的设计流程。

procedure-of-system-design

精确度和召回率

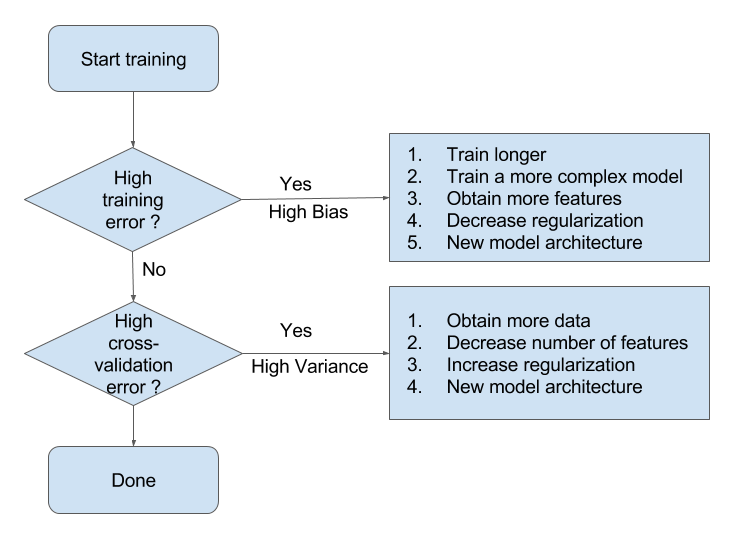
有时准确度（accuracy）并不能全面地衡量一个算法的好坏。例如有二分类问题 \(P(y=1 \vert x) = 0.95\) ，那么一个永远只返回 \(\hat{f}(x) = 1\) 「欺骗性」模型拥有的准确度有 95% 之高。这时我们就需要引入精确度（precision）和召回率（recall）来进一步评价模型的好坏。

对于二分类问题，准确度（accuracy）是指预测结果和标记一致的比例。精确度（precision）是指在预测为「真」的结果中，预测正确的比例。召回率（recall）是指在真正是「真」的结果中，我们预测正确的比例。例解如下图。

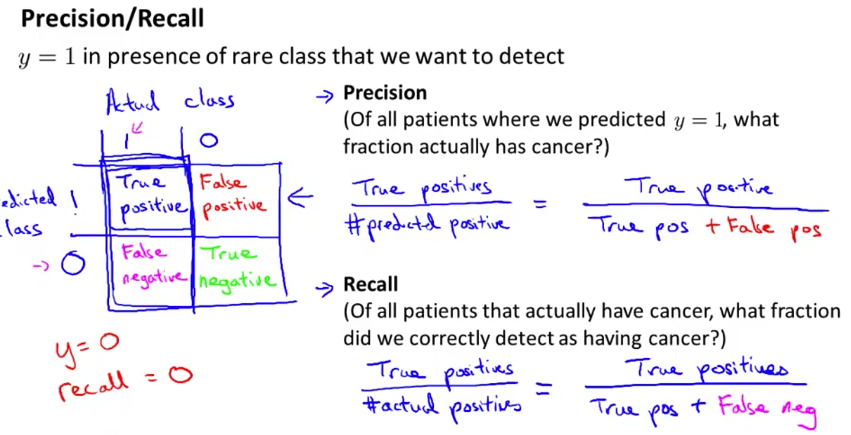
precision-and-recall

精确度和召回率的问题在于，我们无法同时提高两者，这便出现了权衡。这种权衡要针对特定的问题场景来决策，即取决于我们的算法想要达成的目标，以及我们对结果的偏好程度。例如，当我们预测癌症时，一方面是「假阳性」预测会让患者心里受到巨大冲击，另一方面「假阴性」可能使得患者错失治疗时机。

在机器学习领域，一种评价精确度和召回率的方法为：\(F=\dfrac{(a^2+1)P \cdot R}{a^2(P+R)}\) ，其中 \(P\) 和 \(R\) 分别是精确度和召回率。当 \(a=1\) 时为：\(F=2\dfrac{P \cdot R}{P+R}\)。（评价方法有很多，这只是其中一种。）

另外，单纯地增加样本数量并不总是能改进预测结果。如果样本中特征的数量太少，以至于人类专家也无法依据这些有限的特征来预测结果时，增加样本数量的好处可能比较微弱。这时我们需要改进模型。

支持向量机

支持向量机（Support Vector Machine）这个名字太不直观了，要再找点其他资料。

大边界分类（无「核」）

虽然逻辑回归能有效地做二分类，但它存在一个问题——对输入比较敏感。具体而言，当逻辑回归学习到一个决策边界时，该边界实际上存在的可能性很多（很多边界都可以分类样本，这在样本数较少时尤为突出）。

支持向量机改进了逻辑回归的损耗函数（如下图），使得最终学得的边界与两类样本的距离都较大。即，它学到了「某种意义上的」最优分类方法。当然，这种学得的结果对样本的敏感程度由损耗函数中的 \(C\) （相当于正规化参数 \(\dfrac{1}{\lambda}\)）控制。注意下图中 的 \(\mathrm{cost}_1(z)\) 和 \(\mathrm{cost}_2(z)\)。

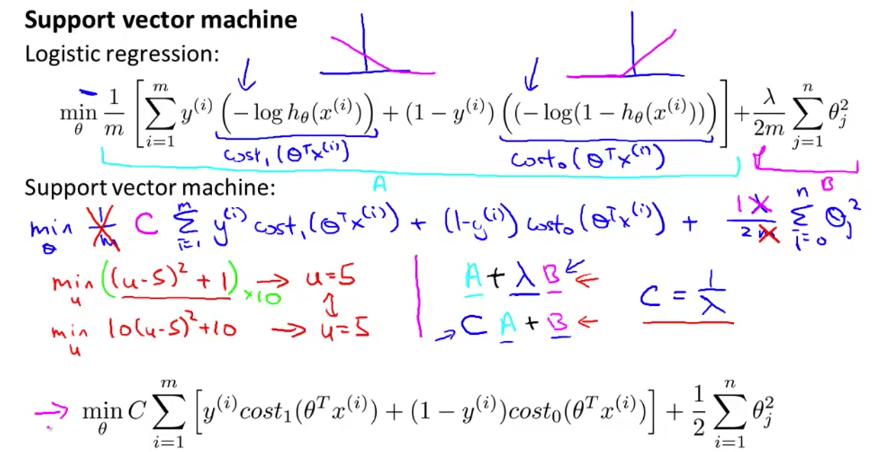
svm-large-margin

但是，为什么支持向量机能学习出大边界呢？

我们知道，向量内积（inner product） \(a{\cdot}b\) 的结果是 \(a\) 在 \(b\) 的方向上的投影长度和 \(b\) 的长度的乘积。而在支持向量机的损耗函数中，我们有针对 \(\theta^{\mathrm{T}}x^{(i)}\) 的判别。将 \(\theta^{\mathrm{T}}x^{(i)}\) 转化为 \(p^{(i)}\cdot \Vert \theta \Vert\) （其中 \(p^{(i)}\) 是 \(x^{(i)}\) 在 \(\theta\) 方向上的投影），我们得到下图中的损耗函数（”s.t.” 的第二部分中 的 if 应为 \(y^{(i)}=0\)）。

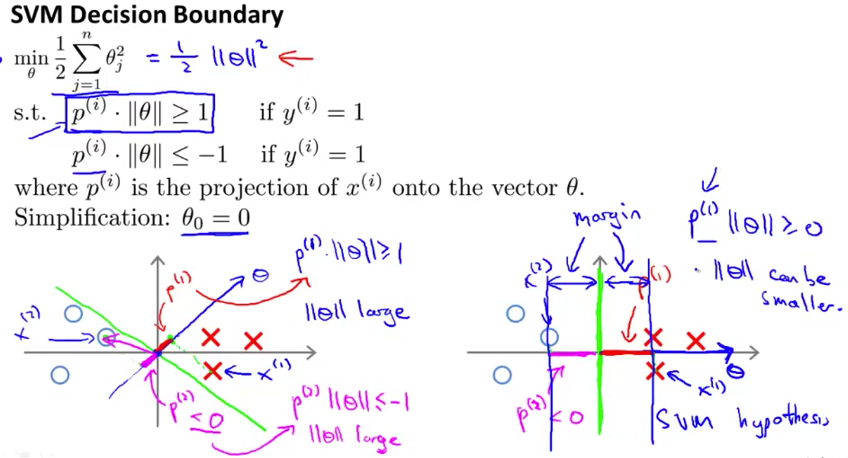
svm-decision-boundary

当算法得到一个「较差」的决策边界时（如上图左半）， \(p^{(i)}\) 较小，要使得 \(p^{(i)}\cdot \Vert \theta \Vert >1\) ，\(\Vert\theta\Vert\) 必然较大。那么要继续优化知道得到如上图右半类似的决策边界时， \(p^{(i)}\) 较大，才达到优化目标。而 \(p^{(i)}\) 实际上就是样本到决策边界的距离，即「边界」。

核：非线性决策边界

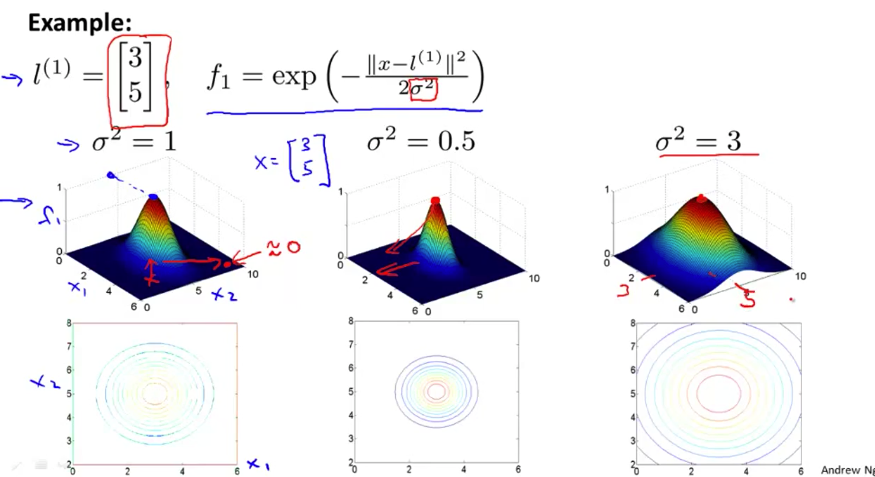
对于拥有非线性决策边界的问题，若用常规方法拟合，那么「特征」会变得非常多。高斯核（Guassian kernel）引入了「相似度」（similarity）来解决这一问题。相似度描述的是坐标系中样本 \(x\) 和「地标」（landmark） \(l^{(i)}\) 之间的关系，具体定义如下。

\[\begin{equation}\begin{aligned} f_i(x) & = \mathrm{similarity}(x, l^{(i)}) \\ & = \mathrm{exp} \left( -\frac{\Vert{x-l^{(i)}}\Vert^2}{2\sigma^2}\right)\\ &= \mathrm{exp}\left(-\frac{\sum_{j=1}^{n}(x_j-l_j^{(i)})^2}{2\sigma^2}\right) \end{aligned}\end{equation}\]

其中 \(x\) 是某样本，\(\sigma\) 是超参数，\(n\) 是样本的维度。在实践中，\(l^{(i)}\) 取自所有样本。当某样本和 \(l^{(i)}\) 「几乎一致」时，我们有 \(f_i \approx 1\) ；否则 \(f_i \approx 0\) 。直观的看，高斯核最终学习出的决策边界是由「同类」样本「聚集」而成的，可以学习出非常复杂的非线性边界。

有了核函数之后，我们的支持向量机预测如下（令 \(f_0=1\)）。

\[\begin{equation}y=\left\{ \begin{aligned} 1; &&& \mathrm{if} \sum_{i=0}^{m}{\theta_i f_i(x)}\geq 0\\ 0; &&& \mathrm{otherwise}. \end{aligned} \right. \end{equation}\]

而训练中我们的优化目标为（其中 \(n\) 往往等于 \(m\)）：

\[\mathop{\min}_{\theta}C \sum_{i=1}^{m}y^{(i)}\mathrm{cost}_0(\theta^\mathrm{T}f^{(i)})+(1-y^{(i)})\mathrm{cost}_1(\theta^\mathrm{T}f^{(i)}) + \frac{1}{2}\sum_{j=1}^{n}\theta_i^2\]

如上一小节所述，超参数 \(C\) 可看做是 \(\dfrac{1}{\lambda}\) 。那么当 \(C\) 较大时，\(\theta\) 倾向于学到大值，偏置（bias）较小，方差（variance）较大。 核函数中的超参数 \(\sigma\) 的影响如下图。当 \(\sigma\) 较大时，\(f\) 的变化比较平缓，可看做核函数的表现力不够，偏置（bias）较大，方差（variance）较小。

svm-kernel-sigma

实践

上一小节的方法有时称作「无核」，有时称作「线性核」（linear kernel）；本小节称作「高斯核」；其他的核还有「多项式核」等。

在选择逻辑回归或 SVM 求解问题时，针对特征数量 \(n\) 和样本数量 \(m\) 的不同我们有以下选择：

  • 当 \(n\) 较大，且相对 \(m\) 也较大（例如 10000 相对于 10-1000）时，使用逻辑回归或无核 SVM。
  • 当 \(n\) 较小，且 \(m\) 与他基本处于同一量级（例如 1-1000 和 10-100000）时，使用基于高斯核的 SVM。
  • 当 \(n\) 较小，而 \(m\) 较大（例如 1-1000 和 50000+）时，增加更多的特征，然后使用逻辑回归或无核 SVM 。

神经网络往往都能较好地运行，只是训练速度可能较慢。

非监督学习

到目前为止我们接触的都是监督学习，本节介绍非监督学习。

聚类：K均值

非监督学习（unsupervised learning）尝试在「未标记」的数据中寻找结构化信息，如聚类（clustering）。

K均值（K-means）是一种典型的聚类算法，它尝试将数据划分为 K 个「类」。对于从 \(m\) 个样例中寻找 \(K\) 个「类」的基本算法如下。

  1. 随机地初始化类 \(\mu^{(1)}, \cdots, \mu^{(K)} \in \mathbb{R}^n\) ；
  2. 重复下面的步骤，直到 \(\mu_k\) 不再变化：
    1. 针对所有的样本 \(x_i\) ，找到与其最近的类 \(\mu_k\)；则样本 \(x_i\) 被分类为 \(k\)，将 \(c_i\) （表示 \(x_i\) 的分类）记为 \(k\)；
    2. 针对所有的类 \(\mu_k$，其值被更新为「被归类到该类的\)x_i$$ 的均值」。

对于上面的步骤，如果没有任何样本被归类到某一类 \(k'\) 中，那么可以删除该分类，或者重新随机地初始化 \(\mu_{k'}\) 。对上面算法的步骤 2.1 ，即优化目标的形式化定义如下：

\[J(c^{(1)}, \cdots, c^{(m)}, \mu^{(1)}, \cdots, \mu^{(K)}) = \frac{1}{m} \sum_{i=1}^{m} \Vert x^{(i)}-\mu_{c^{(i)}}\Vert^2\]

随机初始化 \(\mu^{(1)}, \cdots, \mu^{(K)}\) 的典型方法是，随机地选 \(K\) 个样例，将它们作为 \(\mu_k\) 的初值。但如果运气不好，我们运行算法后得到的可能不是「全局最优」解。这意味着 K均值算法对初值是比较敏感的。一般的解决办法是多次（20-100）运行算法，选取 \(J(c^{(1)}, \cdots, c^{(m)}, \mu^{(1)}, \cdots, \mu^{(K)})\) 最小的作为最终结果。

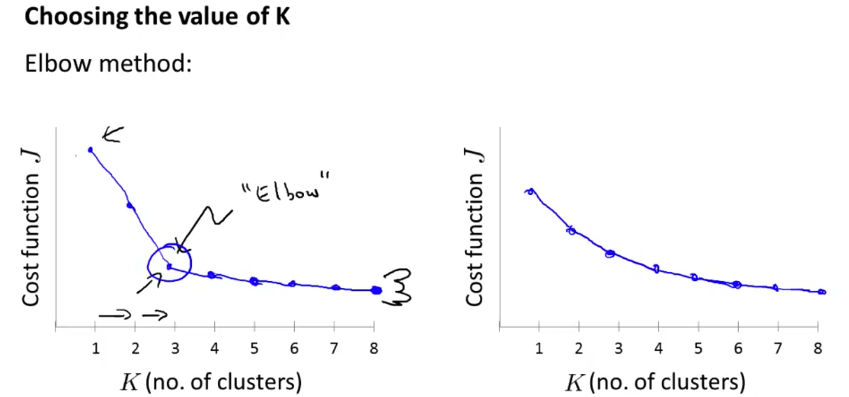
K 均值的另一个问题是如何选择 K 的大小。首先，这有点主观，因为即使面对相同的数据集，不同的人也可能给出不同的答案（结果可能和上图类似）。数学方面的解法称作「肘方法」（Elbow method）。它是尝试若干中 \(K\) 值，将目标函数 \(J\) 绘制成曲线，选取其中 \(J\) 下降速度发生显著变化的点（如下图左半）。但这种方法存在的问题是，可能根本就找不到「肘」（如下图右半）。对于选取 \(K\) 这个问题，最重要的还是要结合我们算法的最终目标。

kmeans-elbow-method

降维：主成分分析

降维（Dimensionality Reduction）是另一种非监督学习方式，主成分分析（principal component analysis）是这类的典型算法。

降维是将高维输入 \(x_i\in\mathbb{R}^n\) 「投影」到低维 \(z_i\in\mathbb{R}^k\) （其中 \(k\leq n\)）。例如下面将二维投影到一维，三维投影到二维。

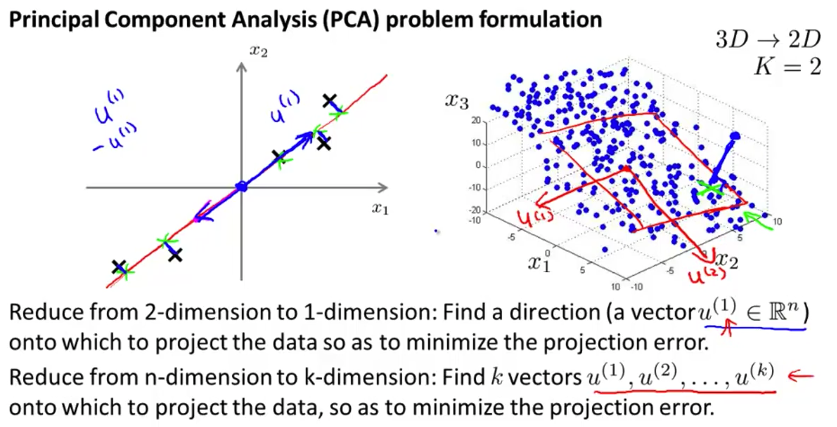
pca-formulation

考虑这是一种非监督学习方法，即我们要从数据中学习到结构化信息，降维学到的就是「\(n\) 维输入其实可以用 \(k\) 维表示」。这种降维的表示之所以能有效地表达信息，是因为原始信息中的维度是存在「冗余」的。例如，当二维中的点基本都在一条线上，或三维中的点都在一个面上。

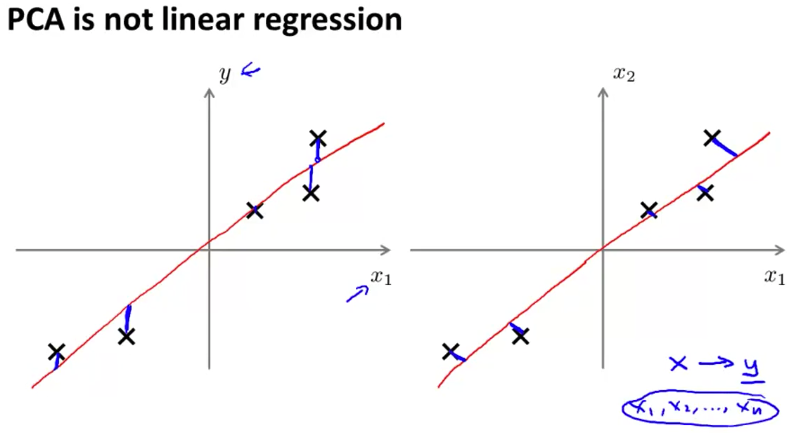
pca-not-linear-reg

值得注意的是，PCA 和线性回归是不同的。线性回归的数据是被标记的，学习目标是对给定的 \(x\) 预测其对应的 \(y\) ；而 PCA 的目标是发现数据中的规律，找到能描述输入的低维向量。如上图，在学习过程中，线性回归的优化目标是对输入 \(x^{(i)}\) ，预测的 \(\hat y^{(i)}\) 数据输出 \(y^{(i)}\) 的距离；而 PCA 的优化目标是输入点 \(x_1^{(i)}, x_2^{(i)}\) 与到向量 \(z\) 的距离。

pca-algo

上图是 PCA 的算法，我们得到的 \(U_{\text{reduce}}^{\mathrm{T}}\) 矩阵 \(k \times n\) 的，它是 \(\begin{bmatrix} u^{(1)}, u^{(2)}, \cdots, u^{(k)} \end{bmatrix}^\mathrm{T}\) 。

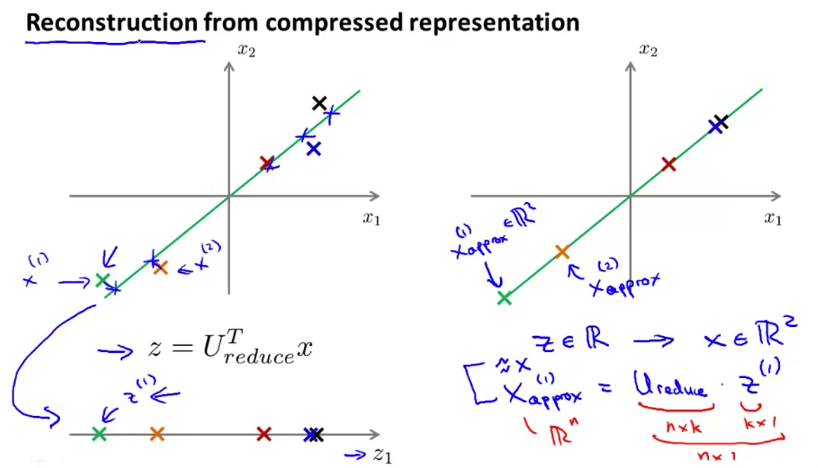
PCA 这样的算法将维度进行了压缩，同时，我们也可以将压缩后的数据 \(z^{(i)}\) 恢复成「近似」的原始数据 \(x_\text{approx}^{(i)}=U_{\text{reduce}} \cdot z^{(i)}\) 。一个二维的示例如下图。注意，恢复之后的数据实际上是 \(\mathbb{R}^n\) 在 \(\mathbb{R}^k\) 中的投影，并不完全等同于原始数据。

pca-reconstruction

下面我们来看 PCA 中的参数 \(k\) ，即主成分的数量。其算法如下。其中的 \(0.01\) 是 \(1-\alpha\) 。$\alpha\(代表降维后保留的程度，该例子中\)\alpha=0.99$$ 。

pca-k

我们使用 PCA 一般有三种原因：通过降维来压缩数据，从而减少磁盘或内存开销；通过降维来加速监督学习；将输入降维到 2 维或 3 维来可视化数据，从而寻找规律。

对于加速监督学习，因为高维度的样例会使得线性回归这样的监督学习方法运行得很慢。对于监督学习的输入 \((x^{(1)}, y^{(1)}); (x^{(2)}, y^{(2)}); \cdots; (x^{(m)}, y^{(m)});\) ，使用 PCA 将 \(x^{(i)} \in \mathbb{R}^n\) 映射为 \(z^{(i)} \in \mathbb{R}^k\) ，那么用得到的新的训练数据 \((z^{(1)}, y^{(1)}); (z^{(2)}, y^{(2)}); \cdots; (z^{(m)}, z^{(m)});\) 训练。在运行测试时，也要执行 \(z^{(i)}=U \cdot x^{(i)}\)，然后再预测。

由于 PCA 能减少特征数量，有人可能会将他用来解决过拟合问题。但这是一种误用，过拟合应当用正规化方法解决。在设计机器学习系统时，如果要使用 PCA ，那么应当弄清楚用与不用的差异在哪里，是不是一定要使用。

异常检测

异常检测（Anomaly Detection）致力于检测一个输入 \(x_{\text{test}}\) 是否「异常」。这种判断基于高斯分布的密度估计（density estimation）。

密度估计的形式化定义为：

  • 选定特征得到输入 \(\{x^{(1)}, \dots, x^{(m)}\}\) ；
  • 拟合得到各个特征的高斯分布参数 \(\mu_1, \mu_2, \cdots, \mu_j; \sigma_1^2, \sigma_2^2, \cdots, \sigma_j^2\) ：\(\displaystyle \mu_j = \frac{1}{m}\sum_{i=1}^m x_j^{(i)},\ \sigma_j^2 = \frac{1}{m}\sum_{i=1}^m(x_j^{(i)} - \mu_j)^2\) ；
  • 对于给定的测试 \(x\) ，计算 \(p(x)\) ，当 \(p(x) \lt \varepsilon\) 时，我们认为发生了异常。这里的 \(\varepsilon\) 是另外的参数。 \(p(x) = \prod_{j=1}^n p(x_j; \mu_j, \sigma_j^2) = \prod_{j=1}^n \frac{1}{\sqrt{2 \pi} \sigma_j} \exp{\left(- \frac{(x_j - \mu_j)^2}{2 \sigma_j^2}\right)}\)

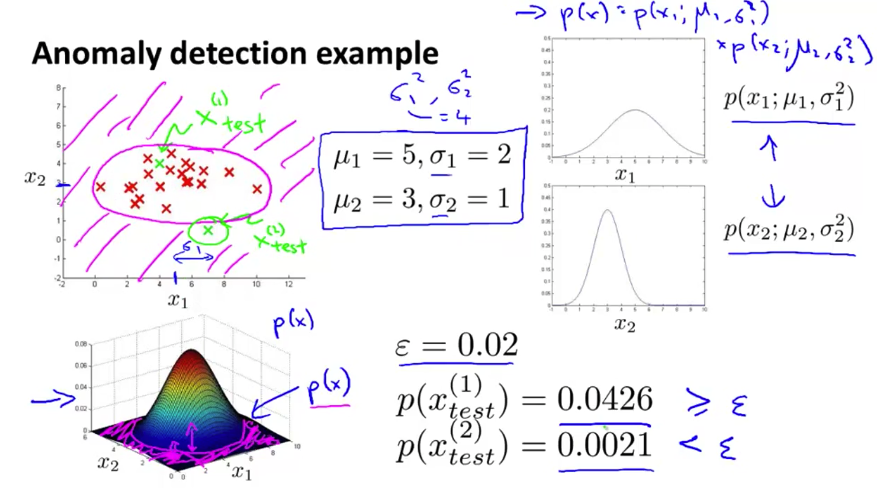
anomaly-detection

在实际应用中 ，我们得到的往往是有标记的数据。由于异常检测往往用于正常数据很多而异常数据很少（例如 10000 vs. 20）的场景中，实施异常检测的常规方法是：选取 60% 的正常数据作为训练集，验证集和测试集均为 20% 的正常数据和 50% 的异常数据。

这让异常检测看起来像是监督学习，但它和常规的监督学习方法还是有差异的。常见的异常检测包括诈骗检测、生产线检测、数据中心的检测；监督学习包括垃圾邮件分类、天气预报、癌症分类。可以看到，当我们认为这两者「相似」时，异常检测更倾向于检测低概率事件，而监督学习更倾向于分类。异常检测中除了异常数据极少，异常数据的「异常类型」各异，这使得常规监督学习方法很难有效地训练；而且新的异常和已有异常可能没什么相似之处，而监督学习希望从样例中发现规律。

前面我们提到异常检测基于高斯分布，当数据分别不够「高斯」时，我们可以应用数学技巧使得数据变成高斯分布，例如 \(\log(x), x^{\alpha}, \cdots\) 。另外，在验证我们的算法时，预测失败的数据可能能指导我们增加新的特征，或是将已有的特征组合起来。

有时我们在异常检测中使用多元高斯分布，形式化定义如下。当 \(p(x)<\varepsilon\) 时为异常。

\[\begin{equation} p(x) = \frac{1}{\sqrt{2 \pi \Sigma}} \exp{\left( -\frac{1}{2} (x-\mu)^\mathrm{T} \Sigma^{-1} (x-\mu) \right)} \\ \mu = \frac{1}{m} \sum_{i=1}^{m} x^{(i)}, \Sigma = \frac{1}{m} \sum_{i=1}^{m} (x^{(i)}-\mu) (x^{(i)}-\mu)^{\mathrm{T}} \end{equation}\]

在异常检测中，我们可以将之前的模型看做是多元高斯分布的一种特例—— \(\Sigma \in \mathbb{R}^{n \times n}\) 是以 \(\sigma_1^2, \sigma_2^2, \cdots, \sigma_n^2 \in \mathbb{R}^{n}\) 为对角的矩阵。这种情况下形成的分布总是轴对称的。

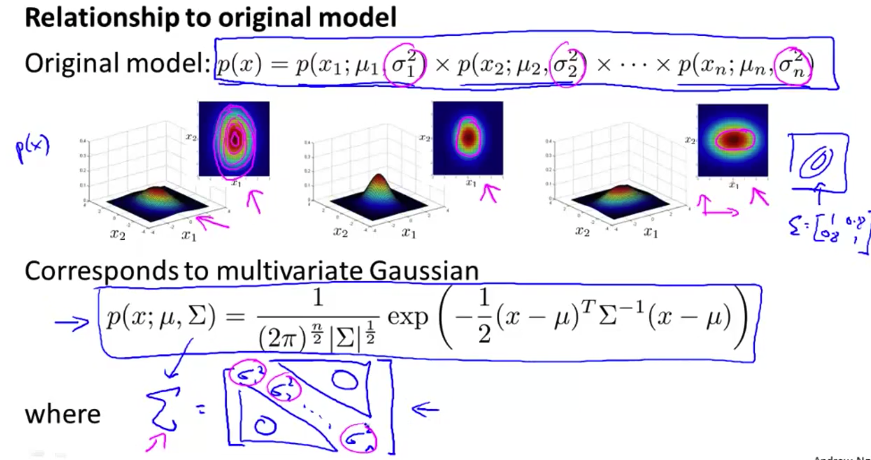
multi-var-gaussian

多元高斯的优势在于它能自动地捕捉特征之间的联系，而原模型需要手动设计。但由于需要计算逆矩阵 \(\Sigma^{-1}\) ，因此计算代价较高，特征太多时可能就不实用。另外，数据量必须大于特征量，否则无法计算 \(\Sigma^{-1}\) （一般在 \(m \gt 10 n\) 时才使用） 。

推荐系统（Recommender Systems）

大规模机器学习

实例：光学字符识别