我们正在向新域名迁移,3秒后自动跳转
We are migrating to new domain, will redirect in 3 seconds
jackwish.net -----> zhenhuaw.me
神经网络量化简介
前言
计划写一系列关于神经网络量化(Neural Network Quantization)的文章已经有一段时间了。这篇神经网络量化简介列出了一些重要的主题。
近年来快速发展的深度学习(Deep Learning)有很多关于量化方法的研究。然而,大多数作者都急于讨论他们的研究细节,以至于新手很难理解研究的立足点。这在一个快速发展的领域可不是好现象。我最初的计划是用便于理解的方式讨论量化的各个方面,包括理论,算术,研究和工业。正如标题所述,本文是关注背景和理论的介绍。
该系列假设读者熟悉机器学习(Machine Learning),神经网络和深度学习相关知识。如有缺乏相关背景知识,Andrew Ng 的机器学习课程是一个非常好的开头。 Google 还提供了基于 TensorFlow 的大量资料。如果您对学院派或理论风格的资料更感兴趣,可以尝试 Goodfellow 的深度学习教材和李飞飞的用于视觉识别的卷积神经网络(即 cs231)。
简介的简介
本节介绍了引入神经网络量化的原因和简要介绍一些主要的研究方向和工业界的解决方案。
为什么需要量化
深度学习已被证明在包括图像分类(Image Classification),目标检测(Object Detection),自然语言处理(Natural Language Processing)等任务上效果很好。大量的应用程序都配备了图像(计算机视觉)相关的深度学习算法,例如 Animoji。而人们使用这些应用程序甚至不知道这种技术的存在。
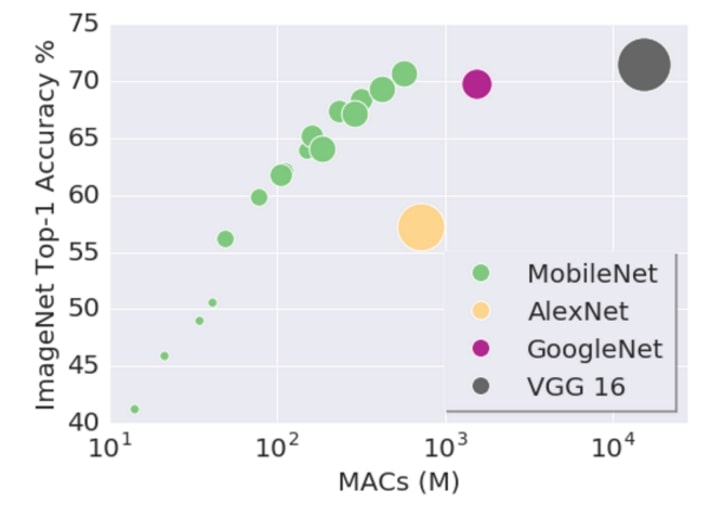 图一:模型 MAC和网络预测准确度。
图一:模型 MAC和网络预测准确度。
自 AlexNet 伊始,基于 ImageNet 的深度学习算法(或模型)改进都和模型大小相关。在如上的由 Google 研究人员给出的 图一 中,垂直方向是网络在给定任务上的效果,横向是网络的大小。通过对比图中 AlexNet,GoogleNet 和 VGG 的趋势不难看出,当模型变大时网络的准确度(accuracy)可能更高。 虽然精心设计的 MobileNet 能在保持较小的体积时仍然具有与 GoogleNet 相当的准确度,不同大小的 MobileNet 本身就表明——也许一个好的模型设计可以改进准确度,但同类模型中仍然是更大的网络,更好的效果!
随着模型预测(predication)越来越准确,网络越来越深,神经网络消耗的内存大小成为问题(图二),尤其是在移动设备上。通常情况下,目前(2019年初)的手机一般配备 4GB 内存来支持多个应用程序的同时运行。而三个模型运行一次通常就要占用1GB内存。
模型大小不仅是内存容量问题,也是内存带宽问题。模型在每次预测时都会使用模型的权重(weights),图像相关的应用程序通常需要实时处理数据,这意味着至少 30 FPS(Frame per Second,每秒帧数)。因此,如果部署相对较小的 ResNet-50 网络来分类,运行网络模型就需要 3GB/s 的内存带宽。网络运行时,内存,CPU 和电池会都在飞速消耗,我们无法为了让设备变得智能一点点就负担如此昂贵的代价。
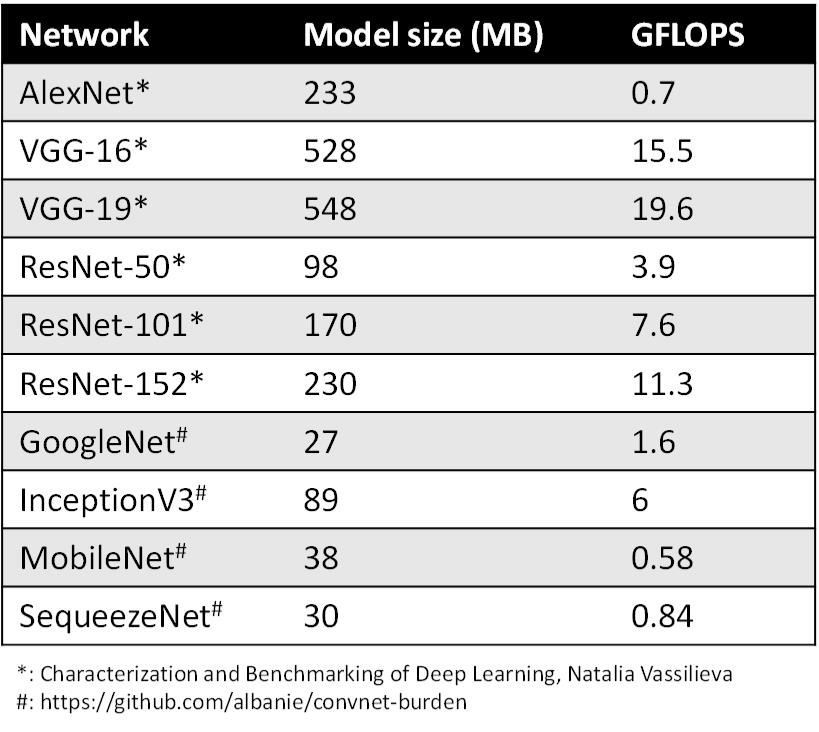 图二:网络的模型大小和 GFLOPS。
图二:网络的模型大小和 GFLOPS。
因此,深度学习领域对这些问题投入了大量的研究资源,主要有两个方面:
- 设计更有效的网络架构,用相对较小的模型尺寸达到可接受准确度,例如 MobileNet 和 SequeezeNet。
- 通过压缩、编码等方式减小网络规模。量化是最广泛采用的压缩方法之一。
这两个方面有时可以共同使用并取得令人瞩目的成果。例如,TensorFlow 量化的MobileNetV1 仅为 4.8MB,这甚至比大多数 GIF 动图还要小,从而可以轻松地部署在任何移动平台上。
量化就是将神经网络的浮点算法转换为定点。这可以在移动手机上实现网络的实时运行,对云计算的部署也有帮助。
学术界的工作
量化有若干相似的术语。低精度(Low precision)可能是最通用的概念。常规精度一般使用 FP32(32位浮点,单精度)存储模型权重;低精度则表示 FP16(半精度浮点),INT8(8位的定点整数)等等数值格式。不过目前低精度往往指代 INT8。
混合精度(Mixed precision)在模型中使用 FP32 和 FP16 。 FP16 减少了一半的内存大小,但有些参数或操作符必须采用 FP32 格式才能保持准确度。如果您对该主题感兴趣,请查看 Mixed-Precision Training of Deep Neural Networks 。
量化一般指 INT8 。不过,根据存储一个权重元素所需的位数,还可以包括:
- 二值神经网络:在运行时权重和激活只取两种值(例如 +1,-1)的神经网络,以及在训练时计算参数的梯度。
- 三元权重网络:权重约束为+1,0和-1的神经网络。
- XNOR网络:过滤器和卷积层的输入是二进制的。 XNOR 网络主要使用二进制运算来近似卷积。
其他一些研究更关注如何压缩整个模型而非存储一个元素的位数。 Deep Compression 是该方向最重要的工作之一,作者将剪枝、量化和编码等技术结合起来,在不显著影响准确性的前提下,将存储需求减少 35x(AlexNet)至 49x(VGG-19)。如图三所示,该论文还表明量化卷积层需要 8 位以避免显着的精度损失,而全连接只需要 4 位。
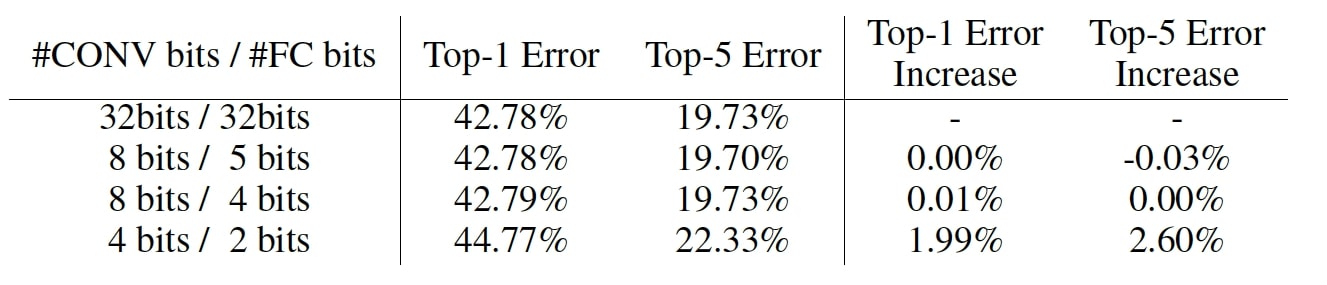 图三:深度压缩中的权重位和网络准确度
图三:深度压缩中的权重位和网络准确度
Cheng Yu 关于模型压缩的调查列出了许多工作,并将它们分类为参数剪枝和共享,低秩分解和稀疏性,传递/紧凑卷积滤波器和知识蒸馏等。
工业界的工作
理论是一回事,实践是另一回事。如果一种技术方法难以推广到通用场景,则需要进行大量的额外支持。花哨的研究往往是过于棘手或前提假设过强,以至几乎无法引入工业界的软件栈。
工业界最终选择了 INT8 量化—— FP32 在推理(inference)期间被 INT8 取代,而训练(training)仍然是 FP32。TensorRT,TensorFlow,PyTorch,MxNet 和许多其他深度学习软件都已启用(或正在启用)量化。
通常,可以根据 FP32 和 INT8 的转换机制对解决方案进行分类。一些框架简单地引入了 Quantize 和 Dequantize 层,当从卷积或全链接层送入或取出时,它将 FP32 转换为 INT8 或相反。在这种情况下,如图四的上半部分所示,模型本身和输入/输出采用 FP32 格式。深度学习框架加载模型,重写网络以插入Quantize 和 Dequantize 层,并将权重转换为 INT8 格式。

其他一些框架将网络整体转换为 INT8 格式,因此在推理期间没有格式转换,如图四的下半部分。该方法要求算子(Operator)都支持量化,因为运算符之间的数据流是INT8。对于尚未支持的那些,它可能会回落到 Quantize/Dequantize 方案。下文的讨论都基于这种方式。
由于 INT8 使用的比特数只有 FP32 的 25% ,在 INT8 和 FP32 之间转换数值的方法非常重要,因为它会显着影响预测精度。
量化的算术
量化过程可以分为两部分:将模型从 FP32 转换为 INT8,以及使用 INT8 进行推理。本节说明这两部分背后的算术原理。如果不了解基础算术原理,在考虑量化细节时通常会感到困惑。
定点和浮点
从事计算机科学的人很少了解算术运算的执行方式。由于量化桥接了固定点(fixed point)和浮点(floating point),在接触相关研究和解决方案之前,有必要先了解它们的基础知识。
定点和浮点都是数值的表示(representation),它们区别在于,将整数(integer)部分和小数(fractional)部分分开的点,点在哪里。定点保留特定位数整数和小数,而浮点保留特定位数的有效数字(significand)和指数(exponent)。
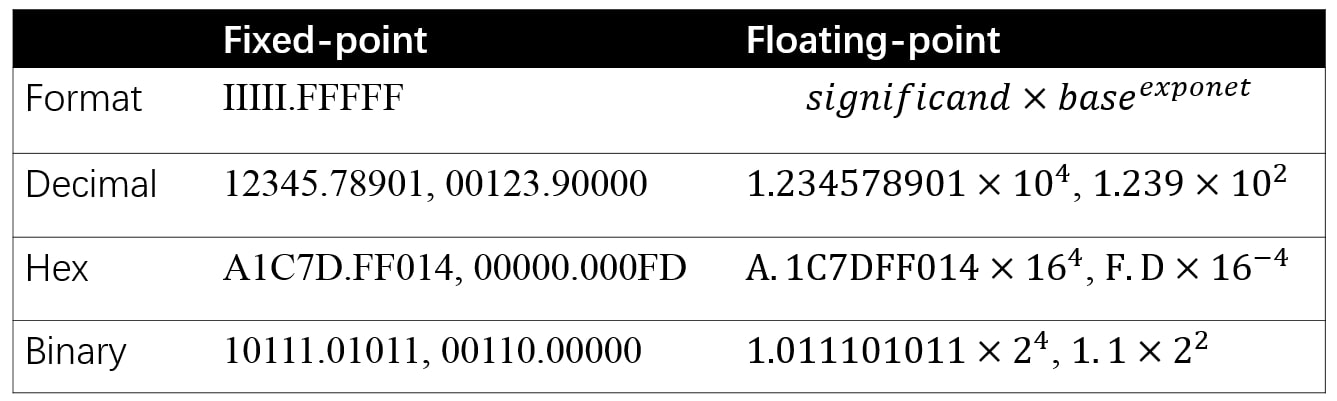 图五:定点和浮点的格式和示例。
图五:定点和浮点的格式和示例。
图五给出了定点和浮点表示的格式和示例。对于定点,\(I\) 表示整数,\(F\) 表示 \(IIIII.FFFFF\) 中的分数。对于浮点数,base分别为二进制、十进制和十六进制格式的 2、10 和 16 。定点和浮点的数值示例在图五中是一一对应的。
在指令集(Instruction Set Architecture)的内置数据类型中,定点是整数,浮点是二进制格式。一般来说,指令集层面的定点是连续的,因为它是整数,且两个邻近的可表示数字的间隙是 1 。另一方面,浮点代表实数,其数值间隙由指数确定,因而具有非常宽的值域(32 位数值最大整数是 \(2 ^ {31} -1\),而浮点值域为 \((2 - 2 ^ { - 23})×2 ^ {127}\)),值越接近零就越准确。一个观察结果是,在给定指数时,浮点在不同范围内拥有数值数量相同数量,如图六。例如,\([1,2)\) 中浮点值的数量与 \([0.5, 1)\)、\([2,4]\)、\([4,8]\)等相同。
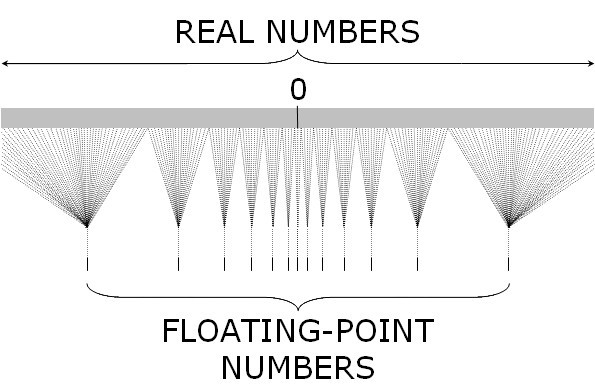 图六:实数和浮点数。
图六:实数和浮点数。
浮点运算可以由整数运算组成,在计算机发展的早期,浮点计算都是用软件在定点硬件上模拟的。下面的等式展示了如何将浮点乘法用定点乘法和加法表示。加法的表示方法要复杂得多,这里不做进一步讨论,有需求的可以参考计算机体系结构相关资料。
\(\begin{align} z &= x \times y \\ z_{significand} \times {base}^{z_{exponent}} &= (x_{significand} \times {base}^{x_{exponent}}) \times (y_{significand} \times {base}^{y_{exponent}}) \\ &= (x_{significand} \times y_{significand}) \times ({base}^{x_{exponent}} \times {base}^{y_{exponent}}) \\ &= (x_{significand} \times y_{significand}) \times {base}^{x_{exponent} + y_{exponent}} \end{align}\) 等式:浮点乘法拆解。
实际上,在上面有效数字的整数乘法之后,当乘法结果相对于表示范围太大时,通常需要重新缩放,如图七。重新缩放移动将有效数字结果的一部分转移到指数,并以最近舍入方法舍入剩余的有效数字。图七的右半部分是一个例子。由于部分数字被舍弃,浮点乘法会丢失一些信息。
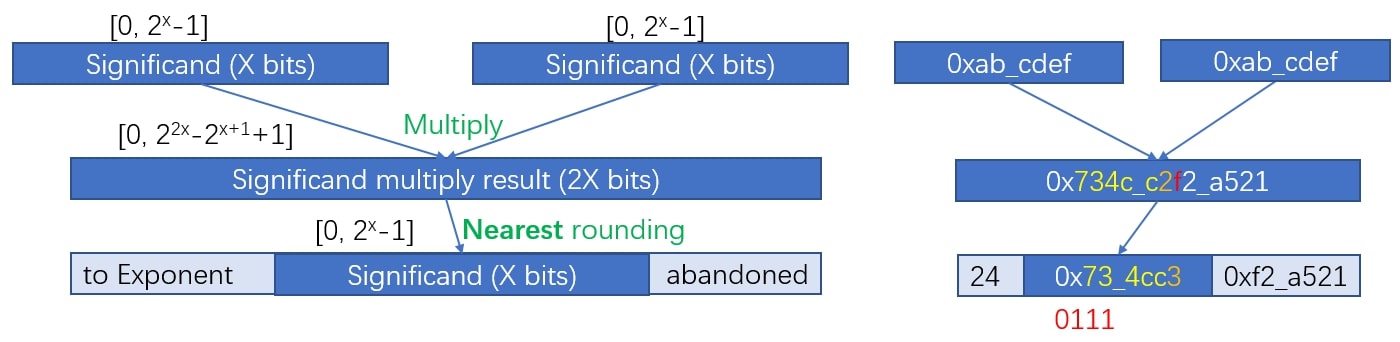 图七:浮点乘法的有效数字部分。
图七:浮点乘法的有效数字部分。
量化浮点
神经网络由浮点运算构成。如定点与浮点所述,FP32 和 INT8 的值域是 \([(2 - 2^{-23}) \times 2^{127}, (2^{23} - 2) \times 2^{127}]\) 和 \([-128, 127]\),而取值数量大约分别为 \(2^{32}\) 和 \(2^8\) 。因此,将网络从 FP32 转换为 INT8 并不像数据类型转换截断那样简单。
幸运的是,神经网络权重的值分布范围很窄,非常接近零。图八给出了 MobileNetV1 中十层(拥有最多值的层)的权重分布。

当值落在 \((-1,1)\) 中,量化浮点使用类似\(x_{float} = x_{scale} \times x_{quantized}\) 的方法将 FP32 映射到 INT8,其中 \(x_{float}\) 表示 FP32 权重,\(x_{quantized}\) 表示量化的 INT8 权重,\(x_{scale}\) 是映射因子(缩放因子)。有时我们不希望将 FP32 零映射到 INT8 零,即数字信号处理中的均一量化和等式5 。
\[x_{float} = x_{scale} \times (x_{quantized} - x_{zero\_point})\]大多数情况下量化选用无符号整数,那么 INT8 值域为 \([0,255]\) 。\(zero\_point\) 在这种情况下更有意义。具体而言,如下面的 等式6-9 所示,量化浮点值可以分为两个步骤:
- 通过在权重张量(Tensor)中找到 min 和 max 值从而确定 \(x_{scale}\) 和\(x_{zero\_point}\)。
- 将权重张量的每个值从 FP32 转换为 INT8 。
注意,当浮点运算结果不等于整数时,需要额外的舍入步骤。例如将 FP32 值域 \([ -1, 1]\) 映射到 INT8 值域 \([0,255]\),有 \(x_{scale} = \frac{2}{255}\),而\(x_{zero\_point} = 255 - \frac{255}{2} \approx 127\)。
量化过程中存在误差是不可避免的,就像数字信号处理中量化一样。图十显示了数字信号处理的量化和误差。
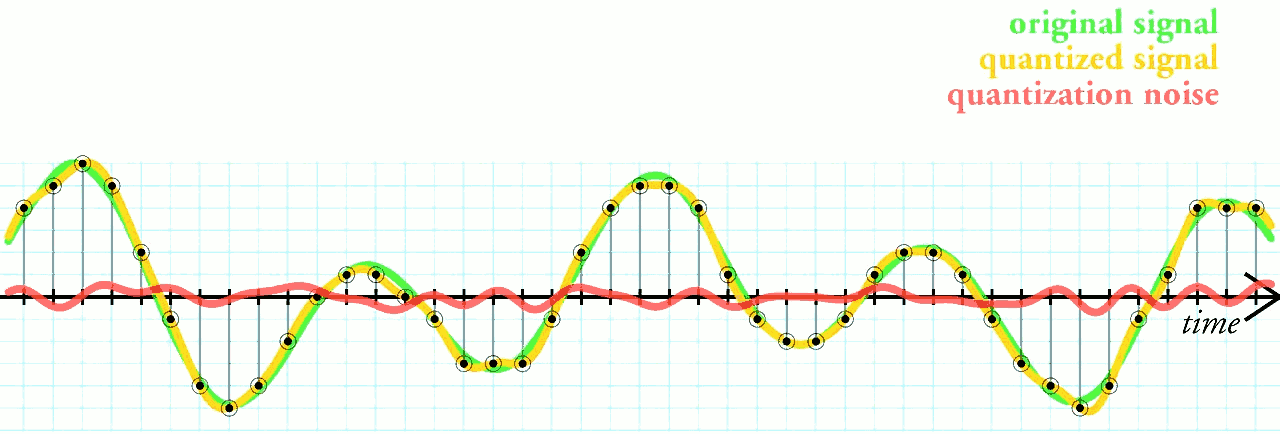 图十:数字信号处理的量化和误差。
图十:数字信号处理的量化和误差。
量化算术
量化的一个重要议题是用量化算术表示非量化算术,即量化神经网络中的 INT8 计算是描述常规神经网络的 FP32 计算。算术表示的原理和定点和浮点 一节中浮点乘法(等式 2-5)过程非常相似。
下面的等式10-16 是量化乘法 \(x_{float} \cdot y_{float}\) 蕴含的原理。等式 15 的 \(Multiplier_{x, y, z}\) 表示等式 14 中的 \(\frac{x_{scale} \cdot y_{scale}} {z_{scale}}\)。对于给定神经网络,输入 \(x\) 、权重 \(y\) 和输出 \(z\) 的缩放因子都是已知的,\(Multiplier_{x, y,z}\) 可在网络运行前预先计算。因此,除了 \(Multiplier_{x, y,z}\) 和 \((x_{quantized} - x_{zero\_point}) \cdot (y_{quantized} - y_{zero\_point})\) 之间的乘法之外,等式 16 中的运算都是整数。
\(\begin{align} z_{float} & = x_{float} \cdot y_{float} \\ z_{scale} \cdot (z_{quantized} - z_{zero\_point}) & = (x_{scale} \cdot (x_{quantized} - x_{zero\_point})) \cdot (y_{scale} \cdot (y_{quantized} - y_{zero\_point})) \\ &= x_{scale} \cdot y_{scale} \cdot (x_{quantized} - x_{zero\_point}) \cdot (y_{quantized} - y_{zero\_point}) \\ z_{quantized} - z_{zero\_point} &= \frac{x_{scale} \cdot y_{scale}}{z_{scale}} \cdot (x_{quantized} - x_{zero\_point}) \cdot (y_{quantized} - y_{zero\_point}) \\ z_{quantized} &= \frac{x_{scale} \cdot y_{scale}}{z_{scale}} \cdot (x_{quantized} - x_{zero\_point}) \cdot (y_{quantized} - y_{zero\_point}) + z_{zero\_point} \\ Multiplier_{x,y,z} &= \frac{x_{scale} \cdot y_{scale}}{z_{scale}} \\ z_{quantized} &= Multiplier_{x,y,z} \cdot (x_{quantized} - x_{zero\_point}) \cdot (y_{quantized} - y_{zero\_point}) + z_{zero\_point} \\ \end{align}\) 等式:量化乘法运算。
对于等式 15可以应用的大多数情况,\(quantized\) 和 \(zero\_point\) 是 INT8,\(scale\) 是 FP32。实际上两个 INT8 之间的算术运算会累加到 INT16 或 INT32,因为 INT8 的值域可能无法保存运算结果。例如,对于 \(x_{quantized} = 20\) 和\(x_{zero\_point} =50\),有 \((x_{quantized} - x_{zero\_point}) = -30\) 超出 INT8 值范围 \([0, 255]\)。
数据类型转换可能将 \(Multiplier_{x,y,z} \cdot (x_{quantized} - x_{zero\_point}) \cdot (y_{quantized} - y_{zero\_point})\) 转换为 INT32 或 INT16,和 \(z_{zero\_point}\) 一道确保计算结果几乎全部落入 INT8 值域 \([0,255]\) 中。
等式 17-26是量化加法算法。它与乘法非常相似,这里不做展开介绍。
\(\begin{align} z_{float} & = x_{float} + y_{float} \\ z_{scale} \cdot (z_{quantized} - z_{zero\_point}) & = (x_{scale} \cdot (x_{quantized} - x_{zero\_point})) + (y_{scale} \cdot (y_{quantized} - y_{zero\_point})) \\ Multiplier_{x,y} &= 2 \cdot max(x_{scale}, y_{scale}) \\ z_{scale} \cdot (z_{quantized} - z_{zero\_point}) &= Multiplier_{x,y} \cdot \left( \frac{x_{scale}}{Multiplier_{x,y}} \cdot (x_{quantized} - x_{zero\_point}) + \frac{y_{scale}}{Multiplier_{x,y}} \cdot (y_{quantized} - y_{zero\_point}) \right) \\ Multiplier_{x} &= \frac{x_{scale}}{Multiplier_{x,y}}; Multiplier_{y} = \frac{y_{scale}}{Multiplier_{x,y}} \\ z_{scale} \cdot (z_{quantized} - z_{zero\_point}) &= Multiplier_{x,y} \cdot \left( Multiplier_{x} \cdot (x_{quantized} - x_{zero\_point}) + Multiplier_{y} \cdot (y_{quantized} - y_{zero\_point}) \right) \\ z_{quantized} - z_{zero\_point} &= \frac{Multiplier_{x,y}}{z_{scale}} \cdot \left( Multiplier_{x} \cdot (x_{quantized} - x_{zero\_point}) + Multiplier_{y} \cdot (y_{quantized} - y_{zero\_point}) \right) \\ Multiplier_{x,y,z} &= \frac{Multiplier_{x,y}}{z_{scale}} \\ z_{quantized} - z_{zero\_point} &= Multiplier_{x,y,z} \cdot \left( Multiplier_{x} \cdot (x_{quantized} - x_{zero\_point}) + Multiplier_{y} \cdot (y_{quantized} - y_{zero\_point}) \right) \\ z_{quantized} &= Multiplier_{x,y,z} \cdot \left( Multiplier_{x} \cdot (x_{quantized} - x_{zero\_point}) + Multiplier_{y} \cdot (y_{quantized} - y_{zero\_point}) \right) + z_{zero\_point} \end{align}\) 等式:量化加法算法。
除了乘法和加法外,还有诸如除法、减法、指数等数值计算,它们都有这些操作都有特定的方法分界为乘法和加法。采用这些方法,量化神经网络可以运行得到和原始网络一样有效的结果。
量化方法的改进
本节探讨工业界提出的解决方案的趋向,它们着力于解决将 FP32 转换为 INT8 时碰到的实际问题。
准确度问题
量化浮点部分中描述的方法非常简单。在深度学习框架的早期开发中,这种简单的方法能快速跑通 INT8 功能,然而采用这种方法的网络的预测准确度通常会出现明显的下降。
如前所述,虽然 FP32 权重的值域很窄,在这值域中数值点数量却很大。以上文的缩放为例,\([-1, 1]\) 值域中 \(2^{31}\)(是的,基本上是总得可表示数值的一半)个 FP32 值被映射到 256 个 INT8 值。再联系量化算术部分讨论的两个重要规则:
- 浮点值越接近零,其值密度越高,对实数的刻画也越准确。
- 均一量化方法将具有动态值密度的浮点映射成具有恒定值密度的定点。
采用普通量化方法时,靠近零的浮点值在量化时没有精确地用定点值表示。因此,与原始网络相比,量化网络预测结果的准确性要差得多。对于均匀量化,这个问题是不可避免的。
等式 4表明值映射的精度受由 \(x_{float}^{min}\) 和 \(x_{float}^{max}\) 得到的 \(x_{scale}\) 的显着影响。并且,如图八所示,权重中邻近 \(x_{float}^{min}\) 和 \(x_{float}^{max}\) 附近的值通常是可忽略的。那么,或许可以选择映射关系中浮点值的 min和 max?
图十展示了可以调整 min/max 来选择一个值域,使得值域的值更准确地量化,而范围外的值映射到定点的 min/max)。例如,当从原始值范围 \([-1,1]\) 中选定\(x_{float}^{min} = -0.9\) 和 \(x_{float}^{max} = 0.8\) ,\([-0.9,0.8]\) 中的值将更准确地映射到 \([0, 255]\) 中,而 \([-1, -0.9]\) 和 \([0.8, 1]\) 中的值分别映射为 \(0\) 和 \(255\)。
值域调整方法
值域调整是另一个机器学习过程,学习的目标是一对能在量化后更准确地运行网络的超参数 min/max。目前已经提出的调整方法可分为训练后量化和训练时量化根据调整何时发生,代表分别为 Nvidia Calibration 和 TensorFlow Quantization-aware Training。
TensorRT、MXNet 等可能在推理环境中部署的框架都配备了校准(Calibration)功能。 图十一的上半部分是校准过程,它与训练过程无关,而是从预训练的模型开始工作。校准通常将 min/max 搜索和量化合并为一个步骤,校准后网络被量化,从而可以直接部署。Nvidia 展示了 TensorRT 校准的架构和相关实验,可参考 GTC2017 的幻灯片 和相关博客。
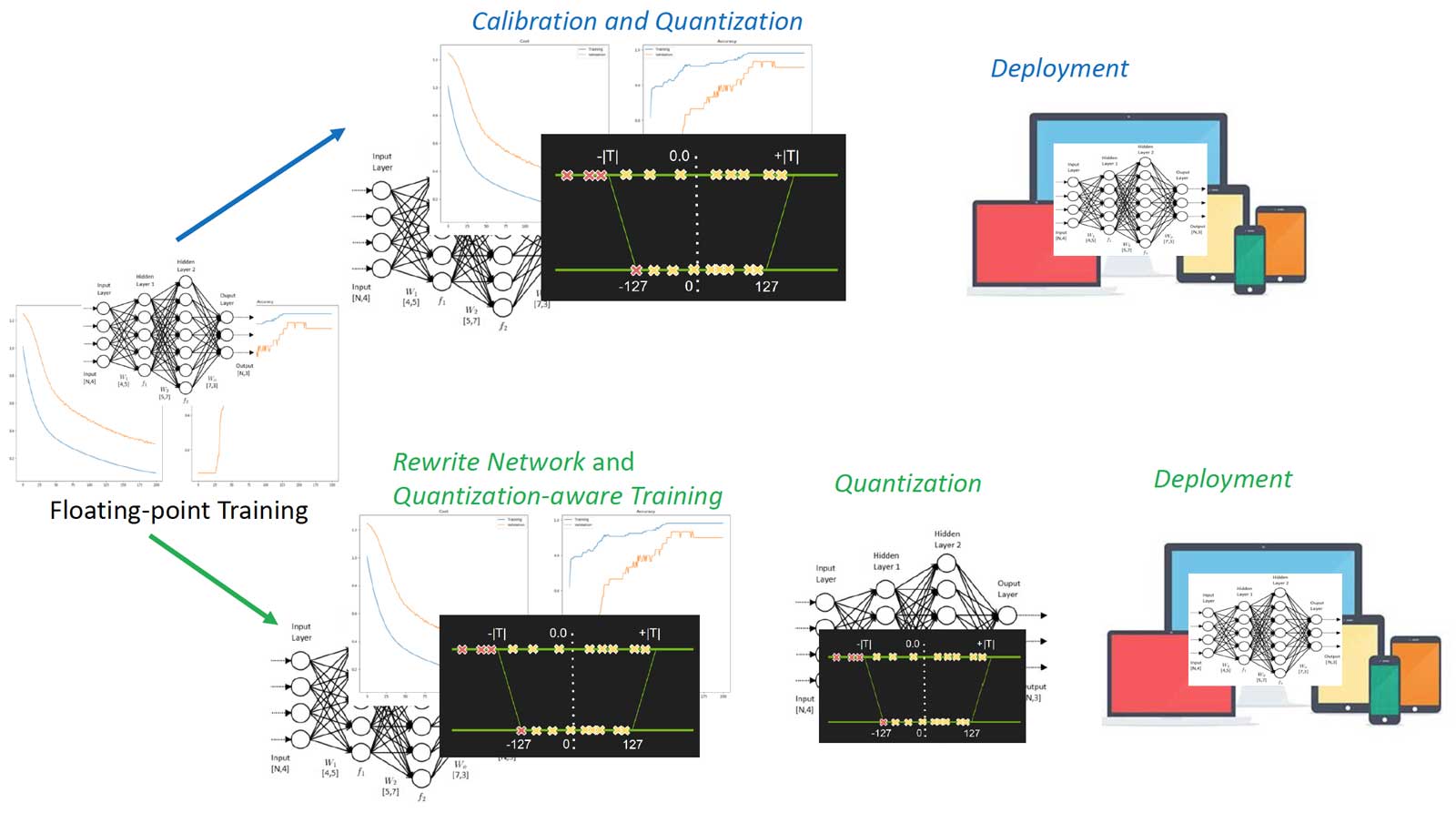 图十一:训练后和训练时量化的过程。
图十一:训练后和训练时量化的过程。
TensorFlow 在支持训练后量化的同时还引入了训练时量化 Quantization-aware Training,其中包括四个步骤:
- 用常规方法训练一个 TensorFlow 浮点模型。
- 用
tf.contrib.quantize重写网络以插入Fake-Quant 节点并训练 min/max。 - 用 TensorFlow Lite 工具量化网络(该工具读取步骤 2 训练的 min/max。
- 用 TensorFlow Lite 部署量化的网络。
步骤 2 是所谓的量化感知训练(Quantization-aware Training),其中网络的前向(forward)模拟 INT8 计算,反向(backward)仍然是 FP32 。图十二左半部分是量化网络,它接收 INT8 输入和权重并生成 INT8 输出。图十二右半部分是步骤 2 重写的网络,其中 Fake-Quant 节点(粉色)在训练期间将 FP32 张量量化为 INT8 (严格来讲仍然是经过 Quantize/Dequantize 过程的 FP32)。
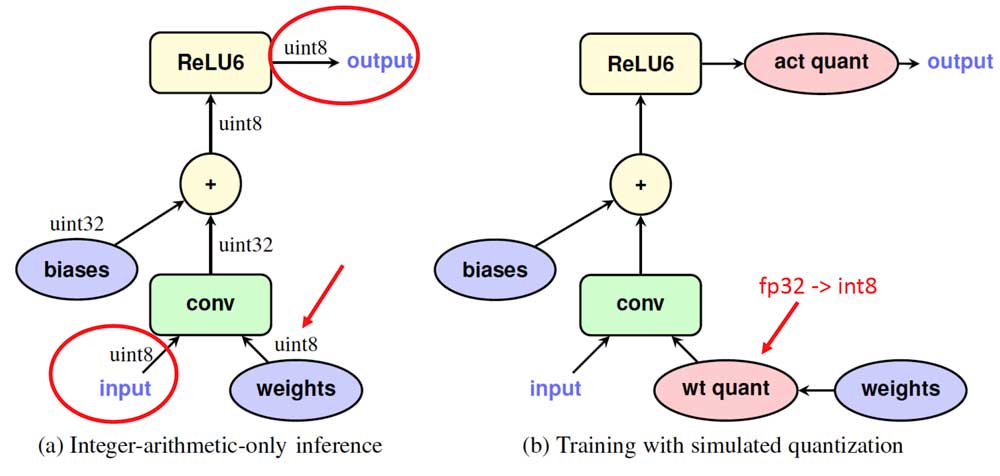 图12:量化感知训练的网络节点示例。
图12:量化感知训练的网络节点示例。
Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference 揭示了量化感知训练的诸多细节。
总结
本文介绍了神经网络量化的背景,探讨了量化的基础算法,并列举了学术界的一些研究和工业界的解决方案。
您可能会问为什么量化是有效的(具有足够好的预测准确度),尤其是将 FP32 转换为 INT8 时已经丢失了信息?严格来说,目前尚未出现相关的严谨的理论。一个直觉解释是,神经网络被过度参数化,进而包含足够的冗余信息,裁剪这些冗余信息不会导致明显的准确度下降。相关证据是,对于给定的量化方法,FP32 网络和 INT8 网络之间的准确度差距对于大型网络来说较小,因为大型网络过度参数化的程度更高。
参考
所有参考文献都列在 Neural Network Quantization Resources 中。



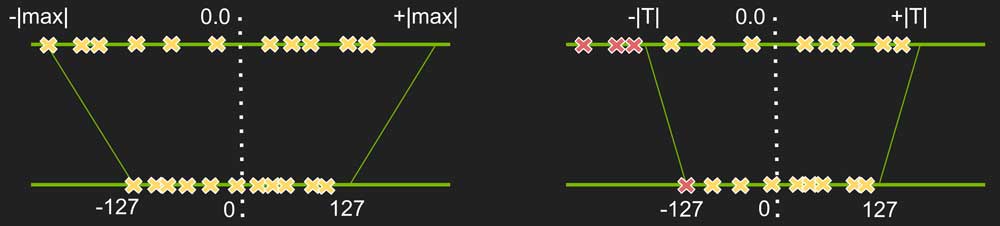 图十:
图十: